Álgebra

La materia de Álgebra Superior nos la imparte el profesor Rafael Sánchez Lara en el horario de Martes y Miercoles de 9:00 a 11:00 am y los Viernes de 10:00 a 11:00 am. El primer día de clase el maestro logro captar toda nuestra atención y lograr que entendiéramos los conceptos que explicaba de una manera practica. Desde el principio hizo hincapié que su principal motivo es que los alumnos estemos felices con su expresión "Que el chavito este feliz".

Durante las clases utilizamos el libro Álgebra y Trigonometria  con geometria analitica 12a. edición  de Swokowski / Cole. Los temas que estamos viendo son: Reducción de polinomios, trinomios, desigualdades e igualdades junto con todos sus casos, vectores y actualmente estamos viendo matrices (para resolver igualdades). Cuando presentó la forma en que calificaría el semestre, el profesor nos menciono que sus participaciones tienen un nombre propio "Chavipoints", este nombre fue dado por los mismos alumnos y su valor monetario es de $50.00 pesos, aunque no esta a la venta.

Como un pequeño dato curioso el profesor pregunto sobre cuanto valor le daríamos a los chavipoints, unos dijeron que $10.00 pesos otros  $100.00 pero cuando me preguntó a mi, al pensar que no creía que tendría un costo barato, dije que yo le daba un valor de  $300.00 pesos y el profesor comento que los Chavitos tramposos siempre le daban un valor caro y quede como un chavito tramposo , por supuesto todo en el sentido de una broma, pero sobre todo no lo soy.

REDUCCIÓN DE POLINOMIO 

Procedimiento:

1. Se reducen por separado los términos semejantes de cada clase, por ejemplo (2x+5x-3x) , (4y-2y-y)
2. A cada clase de aplica la reducción que corresponda según si son signos iguales o distintos.
3. Con los resultados de cada clase se forma la solución final.

Ejemplos: 

A) 5a-6b+8c+9a-20c-b+6b-c 

–> 5a+9a = (5+9)a = 14a

.      -6b-b+6b = (-6-1+6)b = -b

.      8c-20c-c = (8-20-1)c = -13c

Solución:  14a-b-13c

_____________________________________

B) 2/5x^4  -1/2x^3y  +3x^4  -y^4  +5/6y^4  -0.3x^4   -3/5x^3y  -6  +x^3y  -14  +2 1/3y^4

–> 2/5x^4 +3x^4 -3/10x^4 = 31/10x^4

.      -1/2x^3y -3/5x^3y +x^3y = -1/10x^3y

.      -y^4 +5/6y^4 +7/3y^4 = 13/6y^4

.      -6-14 = -20

Solución:  31/10x^4 -1/10x^3y +13/6y^4 -20

——————————————————-

Reducir los polinomios:

1) 7a -9b +6a -4b 

–> 7a +6a = (7+6)a = 13a

.       -9b -4b = (-9 -4)b = -13b

Solución:  13a -13b

——————————————————–

3) 5x -11y -9 +20x -1 -y 

–> 5x +20x = (5+20)x = 25x

.      -11y -y = (-11 -1)y = -12y

.      -9 -1 = -10

Solución:  25x -12y -10

FACTORIZACION  DE TRINOMIOS 

Aprende el método de multiplicación FOIL. El método FOIL (por sus siglas en inglés), el cual significa "primero, exterior, interior y último", y se usa para multiplicar expresiones como (x+2)(x+4). Es de gran ayuda saber cómo funciona dicho método antes de factorizar. Este se realiza de la siguiente manera:

• Multiplica los primeros términos: (x+2)(x+4) = x² + __
• Multiplica los términos exteriores: (x+2)(x+4) = x²+4x + __
• Multiplica los términos interiores: (x+2)(x+4) = x²+4x+2x + __
• Multiplica los últimos términos: (x+2)(x+4) = x²+4x+2x+8
• Simplifica: x²+4x+2x+8 = x²+6x+8

Comprende el proceso de factorización. Cuando multiplicas dos binomios utilizando el método FOIL, el resultado es un trinomio (una expresión con tres términos) de la forma ax²+bx+c, donde a, b y c son números normales. Si te dan una ecuación con esa misma forma, puedes factorizarla para convertirla en dos binomios.

• Si la ecuación no se encuentra escrita de esa forma, reorganiza los términos. Por ejemplo, reescribe3x - 10 + x² como x² + 3x - 10.
• Debido a que el mayor exponente es 2 (x²), este tipo de expresión se denomina "cuadrática".
• Por el momento, solo debes escribir (__ __)(__ __), en el espacio donde planees escribir tu respuesta. Vas a llenar los campos a medida que avances.
• Todavía no escribas + o - en medio de los términos en blanco, ya que desconocemos el signo.
• Para problemas sencillos, donde el primer término del trinomio es x², los términos en las primeras líneas siempre serán x y x. Esos son los factores del término x², ya que x por x = x².
• Nuestro ejemplo x² + 3x - 10 empieza con x², por lo que podemos escribir lo siguiente:
• (x __)(x __)
• Cubriremos problemas más complicados en la próxima sección, incluyendo trinomios que empiecen con un término como 6x² o -x². Por ahora, sigue el ejemplo.
• Si regresas y revisas el método FOIL, te darás cuenta de que al multiplicar los últimos términos obtendrás el término final del polinomio (el que no tiene x). Por ello, para factorizar, necesitarás encontrar dos números que multiplicados den el último término.
• En nuestro ejemplo, x² + 3x - 10, el último término es -10.
• ¿Cuáles son los factores de -10? ¿Qué números multiplicados dan como resultado -10?
• Hay varias posibilidades: -1 x 10, 1 x -10, -2 x 5 y por último 2 x -5. Escribe estos conjuntos de números para que no los olvides.
• Aún no escribas la respuesta. Todavía debe verse así: (x __)(x __).
• Hemos disminuido la búsqueda de los últimos términos a solo un par de posibilidades. Utiliza el ensayo y error para probar cada posibilidad, multiplicando el término exterior por el interior y comparando el resultado con el trinomio. Por ejemplo:
• El problema original tiene un término "x" de 3x, por lo que debemos conseguir ese término con la multiplicación.
• Probemos con -1 y 10: (x-1)(x+10). El exterior + el interior = 10x - x = 9x. No es la respuesta.
• Probemos con 1 y -10: (x+1)(x-10). -10x + x = -9x. Tampoco es la respuesta. De hecho, ya que probamos con -1 y 10, sabemos que si utilizamos 1 y -10, obtendremos la misma respuesta con el signo contrario: -9x en lugar de 9x.
• Probemos con -2 y 5: (x-2)(x+5). 5x - 2x = 3x. Esta respuesta coincide con el polinomio original, por lo que es la respuesta correcta: (x-2)(x+5).
• En casos sencillos como el anterior, cuando no hay una constante al lado del término x², puedes utilizar un atajo: simplemente suma los dos factores y añade una "x" (-2+5 → 3x). Pero este truco no funciona para problemas más complicados, por lo que es bueno recordar la "forma larga" descrita anteriormente.

DESIGUALDADES E IGUALDADES 

IGUALDADES

Una igualdad es una oración matemática que lleva el signo de igual. Por ejemplo:

6 + 4 = 10

x + 6 = 10

·         Una igualdad es una equivalencia entre dos expresiones, las cuales pueden ser numéricas o algebraicas, en cuyo caso hablamos de ecuaciones.  Una igualdad se reconoce por que separa las equivalencias con el símbolo "=" (igual a).

Por ejemplo: 

8 - 6 = 2, es una igualdad numérica, pues como se puede ver tiene el signo "=" entre las expresiones y éstas son equivalente, pues el resultado de la izquierda es equivalente al resultado de la derecha

5x - 6 = 8, es una igualdad conocida como ecuación, pues tiene una incógnita ( "x" en este caso), y existe un valor de "x" que hace que se cumpla la igualdad y que las expresiones de la izquierda, en este caso (5x-6) con las de la derecha, en este caso (8) sean iguales.

                                                                                                                                       

DESIGUALDADES

Por su parte las desigualdades sin expresiones en que una de ellas puede ser llegar a ser menor o igual a la otra, pueden ser numéricas o algebraicas, en cuyo caso hablamos de inecuaciones.  

Los signos de desigualdad son:

≠   no es igual

<   menor que

>   mayor que

≤  menor o igual que

 ≥  mayor o igual que

(La punta del signo siempre señala el menor)

Por ejemplo:

 4 + 3 < 12, es una desigualdad porque primero tiene el símbolo menor que (<) y además la expresión de la izquierda (4+3=7) es menor que la de la derecha, es decir, es desigual

3x - 2 > 4, es una desigualdad porque primero tiene el símbolo mayor que (>) y además existe un conjunto de números que pueden cumplir con la condición de que la expresión (3x - 2) que está a la izquierda de la desigualdad sean mayor que 4 que está a la derecha de la desigualdad.

Propiedades de la Desigualdad (para cualquier número a, b y c)

Comparación	a < b or a = b, or a > b
Adición y Sustracción	1. Si a > b , entonces a + c > b + c y a - c > b - c 2. Si a < b , entonces a + c < b + c y a - c < b - c
Multiplicación y División	1. Si c > 0 y a < d, entonces ac < bc y a/c < d/c 2. Si c > 0 y a > d, entonces ac > bc y a/c > d/c 3. Si c < 0 y a < d, entonces ac > bc y a/c > d/c 4. Si c > 0 y a > d, entonces ac < bc y a/c < d/c
Transitiva	1. Si a < b y b < c, entonces a < c 2. Si a > b y b > c, entonces a > c

*Una desigualdad que tiene variable se llama inecuación.

*Sigua cierta la desigualdad al sumar en ambos lados un número negativo.

*Restar un número es igual que sumar su opuesto.

*Podemos sumar en ambos lados de una desigualdad y sigue cierta.

VECTORES

El concepto de vectores incluye varias cosas, vector es un término que se deriva del vocablo latino y significa “que conduce”. En la física un vector es una cantidad que tiene magnitud, dirección y sentido.

Magnitud:

Es la longitud del vector, para conocerla se necesita saber el origen y el extremo del vector, para poder medir desde donde empieza hasta donde termina. La magnitud es un número.

Dirección:

Es la orientación en el espacio de la recta. La dirección está dada por un ángulo.

Sentido:

Se indica con una flecha, indica hacia que lado se dirige el vector. El sentido está dado por un signo (+ ó -).

Origen:

Es el punto exacto sobre el que actúa el vector.

Concepto de vectores

Un vector se utiliza para representar una magnitud física que tiene dirección y sentido, su expresión geométrica es un segmento de recta con punta de flecha. Algunos ejemplos de magnitudes vectoriales son: fuerza, velocidad, aceleración y desplazamiento.

Se pueden realizar las operaciones con los vectores, las más frecuentes son: suma, resta, producto por un escalar, etc.

• Los vectores se representan por flechas.

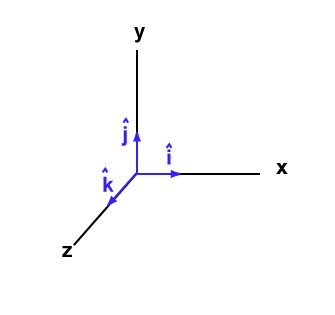
El sistema de referencia que normalmente se usa es el “Sistema de coordenadas cartesianas“, para representar los vectores en el plano cartesiano usamos tres vectores unitarios con dimesión 1, son perpendiculares entre sí y representan cada eje del sistema de referencia.

• Al eje de las “x” se le representa con el vector unitario i.
• Al eje de las “y” se le representa con el vector unitario j.
• Al eje de las “z” se le representa con el vector unitario k.

MATRICES 

Una matriz es un arreglo bidimensional de números consistente en cantidades abstractas que pueden sumarse y multiplicarse entre sí.

Es una disposición de valores numéricos y/o variables (representadas por letras), en columnas y filas, de forma rectangular.

Una matriz es una tabla cuadrada o rectangular de datos (llamados elementos o entradas de la matriz) ordenados en filas y columnas, donde una fila es cada una de las líneas horizontales de la matriz y una columna es cada una de las líneas verticales de la matriz. A una matriz con m filas y n columnas se le denomina matriz m x n; y a m y n se les denomina dimensiones de la matriz.

Las dimensiones de la matriz siempre se dan con el número de fila primero y el número de columnas.

Por lo general se trabaja con matrices formadas por números reales. Las matrices se usan generalmente para describir sistemas de ecuaciones lineales, sistemas de ecuaciones diferenciales o representar una aplicación lineal (dada una base).

Una matriz es una colección ordenada de elementos colocados en filas y columnas, o sea es un arreglo bidimensional de números (llamados entradas de la matriz) ordenados en filas (o renglones) y columnas, donde una fila es cada una de las líneas horizontales de la matriz y una columna es cada una de las líneas verticales. A una matriz con m filas y n columnas se le denomina matriz m por n () donde m y n son números naturales mayores que cero. El conjunto de las matrices de tamaño  se representa como , donde  es el campo al cual pertenecen las entradas. El tamaño de una matriz siempre se da con el número de filas primero y el número de columnas después. Dos matrices se dice que son iguales si tienen el mismo tamaño y las mismas entradas.

Otra definición, muy usada en la solución de sistemas de ecuaciones lineales, es la de vectores fila y vectores columna. Un vector fila o vector renglón es cualquier matriz de tamaño ${\displaystyle 1\times n}$ mientras que un vector columna es cualquier matriz de tamaño ${\displaystyle m\times 1}$.

A las matrices que tienen el mismo número de filas que de columnas, ${\displaystyle m=n\,\!}$, se les llaman matrices cuadradas. y el conjunto se denota ${\displaystyle {\mathcal {M}}_{n\times n}(\mathbb {K} )}$ o alternativamente ${\displaystyle {\mathcal {M}}_{n}(\mathbb {K} )}$.

Notación de Leibniz

Se utiliza un elemento único acompañado de índice y subíndice, de manera tal que el índice indique la columna y el subíndice la fila.

${\displaystyle \mathbb {A} ={\begin{bmatrix}a_{1}^{1}&a_{1}^{2}&a_{1}^{3}\\a_{2}^{1}&a_{2}^{2}&a_{2}^{3}\\a_{3}^{1}&a_{3}^{2}&a_{3}^{3}\end{bmatrix}}}$

Notación de Cauchy

Se utilizan elementos distintos uno para cada columna y a cada elemento se le acompaña de un subíndice que indica la fila del elemento.

Notación más usada

Se utiliza un elemento único acompañado de doble subíndice, de manera tal que el par de valores indique la fila y la columna en ese orden.

A la entrada de una matriz que se encuentra en la fila ${\displaystyle i\,\!}$—ésima y la columna ${\displaystyle j\,\!}$—ésima se le llama entrada ${\displaystyle i,j\,\!}$ o entrada ${\displaystyle (i,j)\,\!}$—ésimo de la matriz. En estas expresiones también se consideran primero las filas y después las columnas.

Casi siempre se denotan a las matrices con letras mayúsculas mientras que se utilizan las correspondientes letras en minúsculas para denotar las entradas de las mismas. Por ejemplo, al elemento de una matriz ${\displaystyle \mathbb {A} }$ que se encuentra en la fila ${\displaystyle i-\,\!}$ésima y la columna ${\displaystyle j-\,\!}$ésima se le denota como ${\displaystyle a_{ij}\,\!}$, donde ${\displaystyle 1\leq i\leq n}$ y ${\displaystyle 1\leq j\leq m}$. Cuando se va a representar explícitamente una entrada la cuál está indexada con un ${\displaystyle i\,\!}$ o un ${\displaystyle j\,\!}$ con dos cifras se introduce una coma entre el índice de filas y de columnas. Así por ejemplo, la entrada que está en la primera fila y la segunda columna de la matriz ${\displaystyle \mathbb {A} }$ de tamaño ${\displaystyle 50\times 100}$ se representa como ${\displaystyle a_{1,2}\,\!}$ mientras que la entrada que está en la fila número 23 y la columna 100 se representa como ${\displaystyle a_{23,100}\,\!}$.

Además de utilizar letras mayúsculas para representar matrices, numerosos autores representan a las matrices con fuentes en negrita para distinguirlas de otros objetos matemáticos. Así ${\displaystyle \mathbb {A} }$ es una matriz, mientras que ${\displaystyle A\,\!}$ es un escalar en esa notación. Sin embargo ésta notación generalmente se deja para libros y publicaciones, donde es posible hacer ésta distinción tipográfica con facilidad. En otras notaciones se considera que el contexto es lo suficientemente claro como para no usar negritas.

Las matrices se suelen notar con letras mayúsculas y sus elementos si son genéricos con minúsculas y un subíndice que indica la fila y columa en que se encuentra, así a23 hace referencia al elemento que se encuentra en la fila 2 columa 3. Una matriz genérica de tres filas y tres columnas, de dimensión 3x3 es:

Dada la matriz ${\displaystyle \mathbb {A} \in {\mathcal {M}}_{3\times 3}(\mathbb {R} )}$

${\displaystyle \mathbb {A} ={\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}}}$

Otra notación, en si un abuso de notación, representa a la matriz por sus entradas, i.e.  o incluso .

Grado de una matriz

El grado de una matriz es la cantidad de elementos que tiene por fila o por columna (si es cuadrada) o la raíz cuadrada del número total de elementos.

Tamaño de una Matriz

La dimensión de una matriz viene dada por el número de filas y columnas que tenga, así una matriz de dimensión 2x3 es una matriz con dos filas y tres columnas. Reiterando, la dimensión de una matriz siempre se da con el número de filas primero y el número de columnas después.

O sea que si se anota  significa que se nombra  a una matriz que tiene 7 filas y 5 columnas. La letra  significa que sus elementos son números reales.

Ejemplo

Dada la matriz ${\displaystyle \mathbb {G} \in {\mathcal {M}}_{4\times 3}(\mathbb {R} )}$

${\displaystyle \mathbb {G} ={\begin{bmatrix}7&5&1\\3&6&4\\1&5&9\\8&3&0\end{bmatrix}}}$

es una matriz de tamaño ${\displaystyle 4\times 3}$. La entrada ${\displaystyle g_{2,3}\,\!}$ es 4.

La matriz ${\displaystyle \mathbb {F} \in {\mathcal {M}}_{1\times 9}(\mathbb {R} )}$

${\displaystyle \mathbb {F} ={\begin{bmatrix}1&4&3&7&5&9&2&8&6\end{bmatrix}}}$

es una matriz de tamaño ${\displaystyle 1\times 9}$: un vector fila con 9 entradas.

Finalmente una matríz genérica se representa: ${\displaystyle \mathbb {A} \in {\mathcal {M}}_{m\times n}(\mathbb {R} )}$

${\displaystyle {\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{bmatrix}}}$

Y una matríz columna genérica 

${\displaystyle {\begin{bmatrix}b_{1}\\b_{2}\\\vdots \\b_{m}\end{bmatrix}}}$