Matemáticas
Su nombre completo es Matemáticas básicas y el docente que nos la imparte es el profesor Mayolo Salvador Islas Chuc. Lunes y miércoles de 15:00 a 17:00 pm nos toca la materia, es bastante dinámica y entretenida, durante la clase y las tareas se utilizan los libros:

Algebra y Trigonometria con geometria analitica
12a. edición de Swokowski / Cole.
Algebra Analitica
de Charles H. Lehmann
Durante las clases estuvimos viendo la reducción de polinomios, trinomios y sus casos especiales, factorizaciones y racionalizaciones. Nos ha marcado diversos ejercicios como todos los casos de facotirizacion de Baldor y del 1.3 al 1.5 de los ejercicios del libro de Lehmann.
En matemáticas básicas, hemos visto los mismos temas que en Álgebra:
FACTORIZACION DE TRINOMIOS
Aprende el método de multiplicación FOIL. El método FOIL (por sus siglas en inglés), el cual significa "primero, exterior, interior y último", y se usa para multiplicar expresiones como (x+2)(x+4). Es de gran ayuda saber cómo funciona dicho método antes de factorizar. Este se realiza de la siguiente manera:
- Multiplica los primeros términos: (x+2)(x+4) = x2 + __
- Multiplica los términos exteriores: (x+2)(x+4) = x2+4x + __
- Multiplica los términos interiores: (x+2)(x+4) = x2+4x+2x + __
- Multiplica los últimos términos: (x+2)(x+4) = x2+4x+2x+8
- Simplifica: x2+4x+2x+8 = x2+6x+8
Comprende el proceso de factorización. Cuando multiplicas dos binomios utilizando el método FOIL, el resultado es un trinomio (una expresión con tres términos) de la forma ax2+bx+c, donde a, b y c son números normales. Si te dan una ecuación con esa misma forma, puedes factorizarla para convertirla en dos binomios.
- Si la ecuación no se encuentra escrita de esa forma, reorganiza los términos. Por ejemplo, reescribe3x - 10 + x2 como x2 + 3x - 10.
- Debido a que el mayor exponente es 2 (x2), este tipo de expresión se denomina "cuadrática".
- Por el momento, solo debes escribir (__ __)(__ __), en el espacio donde planees escribir tu respuesta. Vas a llenar los campos a medida que avances.
- Todavía no escribas + o - en medio de los términos en blanco, ya que desconocemos el signo.
- Para problemas sencillos, donde el primer término del trinomio es x2, los términos en las primeras líneas siempre serán x y x. Esos son los factores del término x2, ya que x por x = x2.
- Nuestro ejemplo x2 + 3x - 10 empieza con x2, por lo que podemos escribir lo siguiente:
- (x __)(x __)
- Cubriremos problemas más complicados en la próxima sección, incluyendo trinomios que empiecen con un término como 6x2 o -x2. Por ahora, sigue el ejemplo.
- Si regresas y revisas el método FOIL, te darás cuenta de que al multiplicar los últimos términos obtendrás el término final del polinomio (el que no tiene x). Por ello, para factorizar, necesitarás encontrar dos números que multiplicados den el último término.
- En nuestro ejemplo, x2 + 3x - 10, el último término es -10.
- ¿Cuáles son los factores de -10? ¿Qué números multiplicados dan como resultado -10?
- Hay varias posibilidades: -1 x 10, 1 x -10, -2 x 5 y por último 2 x -5. Escribe estos conjuntos de números para que no los olvides.
- Aún no escribas la respuesta. Todavía debe verse así: (x __)(x __).
- Hemos disminuido la búsqueda de los últimos términos a solo un par de posibilidades. Utiliza el ensayo y error para probar cada posibilidad, multiplicando el término exterior por el interior y comparando el resultado con el trinomio. Por ejemplo:
- El problema original tiene un término "x" de 3x, por lo que debemos conseguir ese término con la multiplicación.
- Probemos con -1 y 10: (x-1)(x+10). El exterior + el interior = 10x - x = 9x. No es la respuesta.
- Probemos con 1 y -10: (x+1)(x-10). -10x + x = -9x. Tampoco es la respuesta. De hecho, ya que probamos con -1 y 10, sabemos que si utilizamos 1 y -10, obtendremos la misma respuesta con el signo contrario: -9x en lugar de 9x.
- Probemos con -2 y 5: (x-2)(x+5). 5x - 2x = 3x. Esta respuesta coincide con el polinomio original, por lo que es la respuesta correcta: (x-2)(x+5).
- En casos sencillos como el anterior, cuando no hay una constante al lado del término x2, puedes utilizar un atajo: simplemente suma los dos factores y añade una "x" (-2+5 → 3x). Pero este truco no funciona para problemas más complicados, por lo que es bueno recordar la "forma larga" descrita anteriormente.
SISTEMAS DE ECUACIONES
Como es de esperar, el método gráfico consiste en representar las gráficas asociadas a las ecuaciones del sistema para deducir su solución. La solución del sistema es el punto de intersección entre las gráficas. La razón de ello es que las coordenadas de dicho punto cumplen ambas ecuaciones y, por tanto, es la solución del sistema.
Como vamos a trabajar con sistemas de dos ecuaciones lineales con dos incógnitas (x e y), la gráfica de cada ecuación es una recta. Como consecuencia, la intersección de las gráficas es un único punto (a, b)
y la solución del sistema es x = a e y = b. No obstante, si las rectas son paralelas (no se cortan), el sistema no tiene solución, y si son iguales hay infinitas soluciones.
Para poder aplicar el método gráfico debemos saber representar las gráficas de las rectas. Nosotros lo haremos uniendo puntos calculados previamente.
Ejemplo
Resolución:
Lo primero que hacemos es despejar la y en ambas ecuaciones.
Primera ecuación:
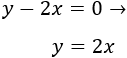
Segunda ecuación:
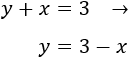
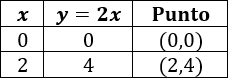
Ahora vamos a calcular unos cuantos puntos de las dos funciones para representarlas. Utilizamos, por ejemplo, x = 0 y x = 2.
Para la primera función tenemos la tabla
Para la segunda función tenemos la tabla (utilizando los mismos valores para x):
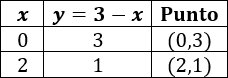
Representamos los puntos de las tablas y los unimos:
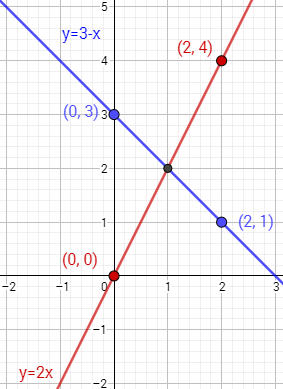
La solución del sistema es el punto donde las gráficas se cortan:
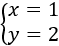
Ejemplo de sistemas de ecuación de 2x2

SUSTITUCIÓN
Despejamos en la primera ecuación la :
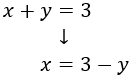 Y la sustituimos en la segunda:
Y la sustituimos en la segunda:
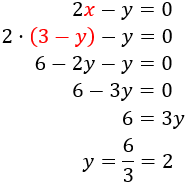 Calculamos sabiendo :
Calculamos sabiendo :
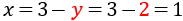 Por tanto, la solución del sistema es
Por tanto, la solución del sistema es
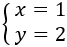
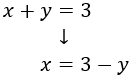
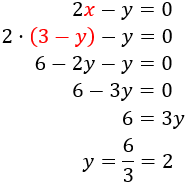
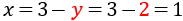
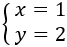
IGUALACIÓN
Despejamos en ambas ecuaciones la
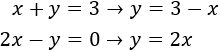 Como , igualamos las expresiones y resolvemos la ecuación:
Como , igualamos las expresiones y resolvemos la ecuación:
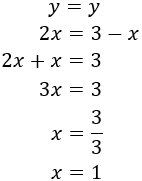 Ahora, sustituimos el valor de la incógnita en la primera de las ecuaciones anteriores para calcular :
Ahora, sustituimos el valor de la incógnita en la primera de las ecuaciones anteriores para calcular :
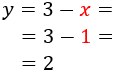 Por tanto, la solución del sistema es
Por tanto, la solución del sistema es
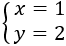
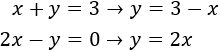
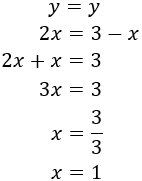
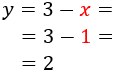
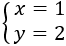
REDUCCIÓN
Para sumar las ecuaciones y que desaparezca una de las dos incógnitas, los coeficientes de dicha incógnita deben ser iguales pero de signo distinto. Para ello, multiplicamos por -2 la primera ecuación.
Después, sumamos las ecuaciones y resolvemos la ecuación obtenida:
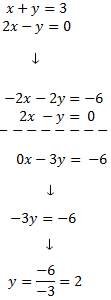 Finalmente, sustituimos el valor de en la primera ecuación y la resolvemos:
Finalmente, sustituimos el valor de en la primera ecuación y la resolvemos:
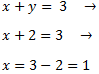 Por tanto, la solución del sistema de ecuaciones es
Por tanto, la solución del sistema de ecuaciones es
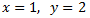
Después, sumamos las ecuaciones y resolvemos la ecuación obtenida:
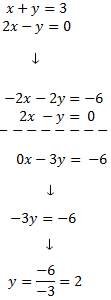
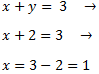
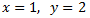
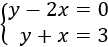


Comentarios
Publicar un comentario